Longest run of heads - Halil Ibrahim Gunduz

% % LongestrunofHeads
clear; close; clc;

In a (fair) coin toss experiment, the coin is tossed n times. The result is a series of heads (H) and tails (T). A subsequence of consecutive heads (tails) is called heads (tails): Sequence 1: THHHHTTTTHHHHTTTTHHHHTH... Sequence 2: THTHTTTHTTTTTHTHTTTHTTH... from https://www.maa.org/sites/default/files/images/upload_library/22/Polya/07468342.di020742.02p0021g.pdf we analyze which of the sequences is more likely to have arisen from actual coin tossing and which one is the imposter?

% We solve this famous problem from Davidson, R., & MacKinnon, J. G. (1993)
% Estimation and inference in econometrics (Vol. 63). New York: Oxford:

% "A well-worn example of a nonstochastic probability limit is given by
% considering the limit of the sequence of proportions of heads in a series
% of independent tosses of an unbiased coin. It is worth demonstrating
% formally that the probability limit is indeed one-half, since this will
% give us the opportunity to see some useful techniques of proof and
% acquire some intuition about how probability limits differ from ordinary
% ones."

tic
rng(729183,'multFibonacci')                                                 % Control random number generator

Our aim is show the convergence in probability of 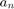$a_{n}$ to 1/2 for a unbiased coin:

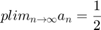
$plim_{n \rightarrow \infty} a_{n}=\frac{1}{2}$

In case of biased coin, this plim is unvalid.

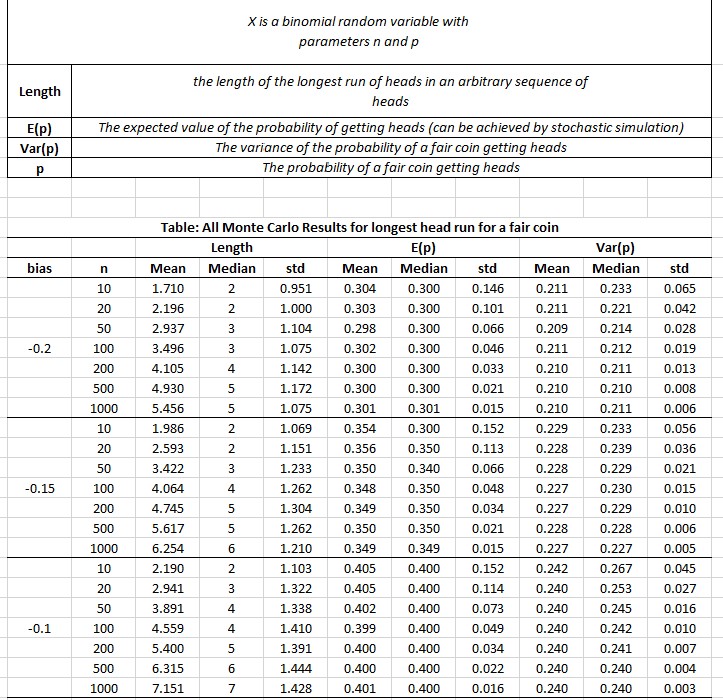
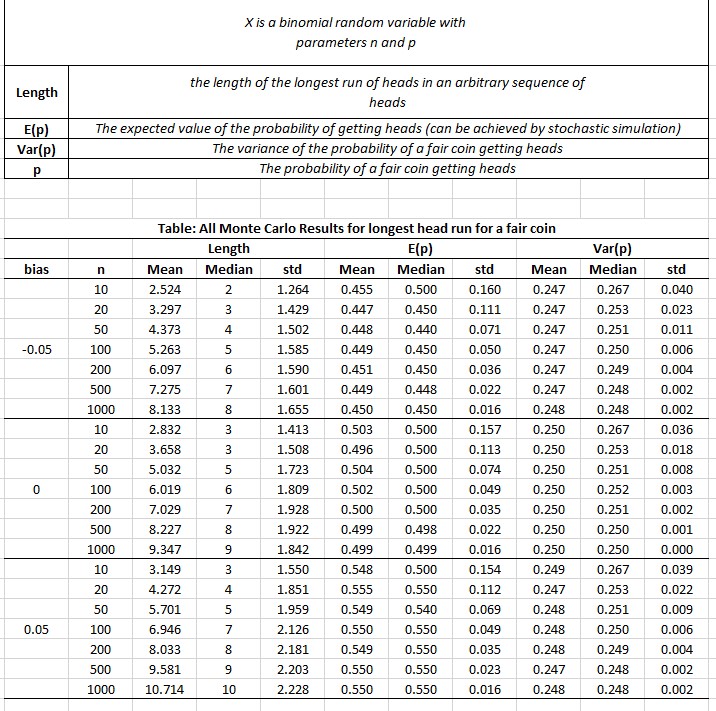
n=[10 20 50 100 200 500 1000];                                              % number of trials
p=0.5;                                                                      % probability of heads(tails)
bias=[-0.2 -0.15 -0.1 -0.05 0 0.05 0.1 0.15 0.2];                           % we inject bias
MC=1000;                                                                    % the number of Monte carlo simulation experiments
nn=size(n,2);
Seq=cell(nn,1);                                         % sets of random sequences of heads and tails for any value of n.
longest=zeros(nn,MC);
theLength=zeros(nn,3);                                  % the length of the longest run of heads in an arbitrary sequence of heads and tails.
Mu_mc=zeros(nn,MC);Var_mc=zeros(nn,MC);
theMu=zeros(nn,3);theVar=zeros(nn,3);
bb=size(bias,2);
sonuc=cell(bb,3);
for b=1:bb
    for j=1:nn
        trial=zeros(n(j),1);
        for i=1:n(j)
            trial=rand(i,MC)<(bias(b)+p);
        end
        Seq{j,1}=double(trial);
        for mc=1:MC
            if Seq{j,1}(:,mc)==0
                longest(j,mc)=0;
            else
                longest(j,mc)=max(accumarray(nonzeros((cumsum(~Seq{j,1}(:,mc))+1).*Seq{j,1}(:,mc)),1));
            end
            Mu_mc(j,mc)=mean(Seq{j,1}(:,mc));
            Var_mc(j,mc)=var(Seq{j,1}(:,mc));
        end
        theLength(j,:)=[mean(longest(j,:)) median(longest(j,:)) std(longest(j,:))];
        theMu(j,:)=[mean(Mu_mc(j,:)) median(Mu_mc(j,:)) std(Mu_mc(j,:))];
        theVar(j,:)=[mean(Var_mc(j,:)) median(Var_mc(j,:)) std(Var_mc(j,:))];
    end
        sonuc{b,1}=theLength;
        sonuc{b,2}=theMu;
        sonuc{b,3}=theVar;
end
Sonucxlsx=cell2mat(sonuc) ;                                                 % All outcomes of the Monte Carlo Simulation values
toc

Elapsed time is 167.833585 seconds.