Python Object-Oriented Programming (OOP): What can we say about US housing price inflation?¶
Introduction¶
In this project, we analyze housing price inflation in the USA using object-oriented programming (OOP). Our econometric strategy is the autoregressive modeling approach. We use OOP to apply the AR process to a time series data. We consider a housing proce index:
$y_{t}$: S&P/Case-Shiller U.S. National Home Price Index
You can acess this data from https://fred.stlouisfed.org/series/CSUSHPISA. For more information regarding the index, please visit Standard & Poor's (https://www.spglobal.com/spdji/en/documents/methodologies/methodology-sp-corelogic-cs-home-price-indices.pdf). There is more information about home price sales pairs in the Methodology section. Copyright, 2016, Standard & Poor's Financial Services LLC. Reprinted with permission.
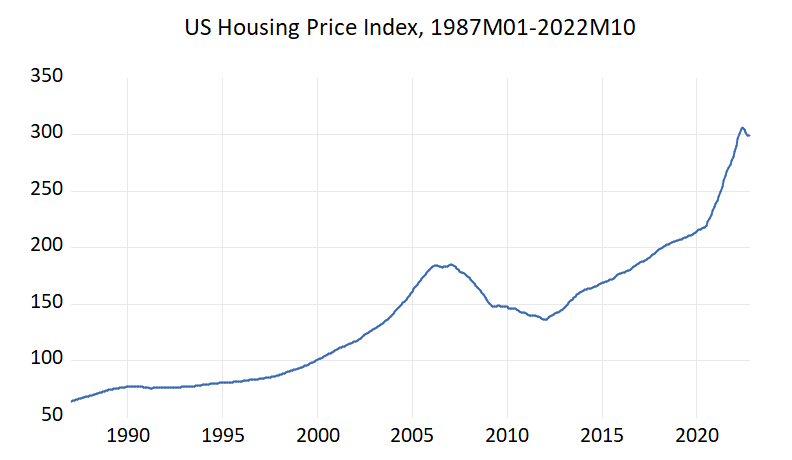
From this figure, also from unit root tests, we understand this variable is nonstationary in level. Thus, we use first difference of LOG = percentage change:
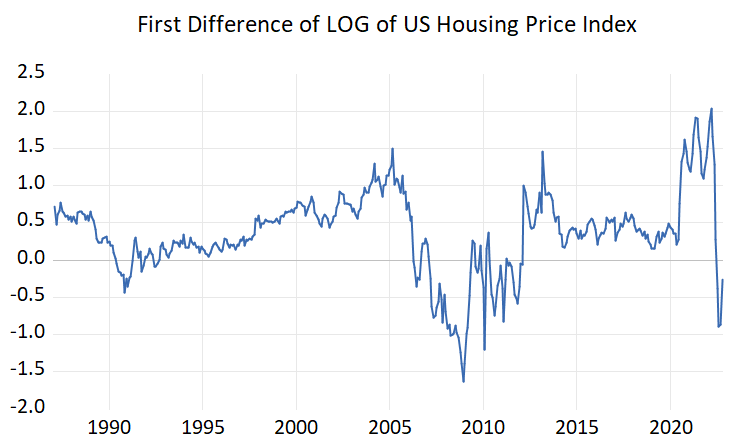
Let's make it the subject of another series of articles that this graphic tells us about the US economy. Now our priority is the processing of AR models with OOP. Let's download the necessary packages:
import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt
from numpy import hstack, nan, tile, vstack, zeros
try:
import seaborn
except ImportError:
pass
Defining an AR Class¶
Let's create an AR class and define the methods and basic building blocks within this class.
class AR(object):
def __init__(self, data=None, ar_order=1):
self._data = data
self._ar_order = ar_order
self._sigma2 = 1
self._T = None
self._X = None
self._y = None
self._roots = None
self._abs_roots = None
self._fit_values = None
self._parameters = None
self._errors = None
if data is not None:
self._generate_regressor_array()
@property
def data(self):
return self._data
@property
def ar_order(self):
return self._ar_order
@property
def parameters(self):
return self._parameters
@property
def sigma2(self):
return self._sigma2
@property
def roots(self):
return self._roots
@property
def abs_roots(self):
return self._abs_roots
@property
def fit_values(self):
if self._fit_values is None:
self.estimate()
return self._fit_values
@data.setter
def data(self, value):
self._data = value
self._generate_regressor_array()
if self._parameters is not None:
self._update_values()
@parameters.setter
def parameters(self, value):
if value.ndim not in (1, 2):
raise ValueError("parameters must be a vector")
value = value.ravel()[:, None]
if value.shape[0] != (self._ar_order + 1):
raise ValueError(f"parameters must have {self._ar_order + 1} elements.")
self._parameters = value
self._update_roots()
@sigma2.setter
def sigma2(self, value):
if value <= 0.0:
raise ValueError("sigma2 must be positive")
self._sigma2 = value
def _generate_regressor_array(self):
p = self._ar_order
T = self._T = len(self._data)
x = np.ones((T - p, p + 1))
y = self._data[:, None]
for i in range(p):
x[:, [i + 1]] = y[p - i - 1:T - i - 1, :]
self._y = self.data[p:, None]
self._X = x
def _update_roots(self):
if self._ar_order > 0:
coeffs = self._parameters[1:].ravel()
char_equation = np.concatenate(([1], -1.0 * coeffs))
self._roots = np.roots(char_equation)
self._abs_roots = np.absolute(self._roots)
else:
self._roots = None
self._abs_roots = None
def _update_values(self):
fv = self._X.dot(self._parameters)
e = self._y - fv
self._sigma2 = np.dot(e.T, e) / len(e)
self._errors = vstack((tile(nan, (self._ar_order, 1)), e))
self._fit_values = vstack((tile(nan, (self._ar_order, 1)), fv))
def estimate(self, insample=None):
x = self._X
y = self._y
# y = y[:, None]
p = self._ar_order
if insample is not None:
x = x[:(insample - p),:]
y = y[:(insample - p)]
xpxi = np.linalg.pinv(x)
self.parameters = xpxi.dot(y)
def forecast(self, h=1, insample=None):
tau = self._X[:, 1:].shape[0]
fcasts = hstack((self._X[:, :0:-1], zeros((tau, h))))
p = self._ar_order
params = self._parameters
for i in range(h):
fcasts[:, p + i] = params[0]
for j in range(p):
fcasts[:, p + i] += params[j + 1] * fcasts[:, p + i - (j + 1)]
fcasts = vstack((tile(nan, (p, p + h)), fcasts))
if insample is not None:
fcasts[:insample, :] = nan
return fcasts[:, p:]
def forecast_plot(self, h=1, show=True, show_errors=False):
fcasts = self.forecast(h=h)
T = self._T
p = self._ar_order
aligned = zeros((T + h, 2))
aligned[:T, 0] = self._data
aligned[-T:, 1] = fcasts[:, -1]
aligned = aligned[p:T, :]
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
if show_errors:
ax.plot(aligned[:, 0] - aligned[:, 1])
else:
ax.plot(aligned)
if show:
plt.show(fig)
return fig
def hedgehog_plot(self, h=1, show=True, skip=0):
fcasts = self.forecast(h=h)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(self._data)
data = self._data
for i in range(0, self._T, skip + 1):
x = i + np.arange(h + 1)
y = hstack((data[[i]], fcasts[i]))
ax.plot(x, y, 'r')
ax.autoscale(tight='x')
fig.tight_layout()
if show:
plt.show(fig)
return fig
def simulate(self, T=500, burnin=500):
tau = T + burnin + self._ar_order
e = rnd.standard_normal((tau,))
y = zeros((tau,))
p = self._ar_order
for t in range(p, tau):
y[t] = self._parameters[0]
for i in range(p):
y[t] += self._parameters[i + 1] * y[t - i - 1]
y[t] += e[t]
return y[-T:]
Load the data¶
import pandas as pd
housinginf_excel = pd.read_excel("housinginf.xls", skiprows=10,
index_col="observation_date")
# print(gs10_excel)
data = housinginf_excel.housinginf.to_numpy()
We estimate the following model with the estimation and forecasting methods we defined in the AR class: $$y_{t}=\alpha_{0}+\alpha_{1}y_{t-1}+\alpha_{2}y_{t-2}+\alpha_{3}y_{t-3}+\varepsilon_{t}$$
T = 429
ar_order = 3
in_sample = 10
h=5
# Initialize the object
# ar = AR(activity, ar_order)
ar=AR(data,ar_order)
ar.estimate()
forecasts = ar.forecast(h,in_sample)
Let's plot the forecasting error data with the real data:
p = ar_order
aligned = zeros((T + h, 2))
aligned[:T, 0] = data
aligned[-T:, 1] = forecasts[:, -1]
aligned = aligned[p:T, :]
plt.plot(np.arange(1, T-ar_order+1), aligned)
plt.show()
In this figure, the blue series represents the actual data, while the orange series represents the forecast error data. Note: The information in the link below was used in the creation of the OOP for the AR modeling approach: https://www.kevinsheppard.com/teaching/python/notes/#notes